Ncert Solutions For Class 6 Maths Chapter 14 Practical Geometry Ex 14.5 Practical Geometry Exercise 14.5 Ncert Solutions For Class 6 Maths Chapter 14 Practical Geometry Ex 14.5 Chapter 14 Practical Geometry Class 6 Chapter 14 Maths Chapter 14 Class 6 Maths Maths Class 6 Chapter 14 Maths Chapter 14 Class 6 Ncert Maths Class 6 Chapter 14 Ncert Solutions For Class 6 Maths Chapter 14 Practical Geometry Class 6 Maths Chapter 14 Practical Geometry Ex 14.5 Class 6 Maths Ncert Solutions
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5
Question 1.
Draw AB¯¯¯¯¯¯¯¯ of length 7.3 cm and find its axis of symmetry.
Solution :
Step 1. Draw a line segment AB¯¯¯¯¯¯¯¯ of length 7.3 cm.
Step 2. With A ascentere, using compasses, drawthe circle. The radius of this circle should be more than half of the length of AB¯¯¯¯¯¯¯¯.
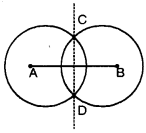

Step 3. With the same radius and with B as a centre, draw another circle using compasses. Let it cut the previous circle at C and D.
Step 4. Join CD. Then, CD¯¯¯¯¯¯¯¯ is the axis of symmetry of AB¯¯¯¯¯¯¯¯.
Question 2.
Draw a line segment of length 9.5 cm and construct its perpendicular bisector.
Solution :
Step 1. Draw a line segment AB¯¯¯¯¯¯¯¯ of length 9.5 cm.
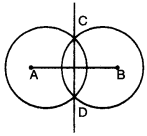

Step 2. With A as a centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of AB¯¯¯¯¯¯¯¯.
Step 3. With the same radius and with B as a centre, draw another circle using compasses. Let it cut the previous circle at C and D.
Step 4. Join CD. Then CD¯¯¯¯¯¯¯¯ is the perpendicular bisector of the line segment AB¯¯¯¯¯¯¯¯.
Question 3.
Draw the perpendicular bisector of XY¯¯¯¯¯¯¯¯ whose length is 10.3 cm.
(a) Take any point P on the bisector drawn. Examine whether PX = PY.
(b) If M is the midpoint of XY¯¯¯¯¯¯¯¯, what can you say about the lengths MX and XY ?
Solution :
Step 1. Draw a line segment XY¯¯¯¯¯¯¯¯ of length 10.3 cm.
Step 2. With X as a centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of XY¯¯¯¯¯¯¯¯.
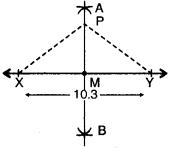

Step 3. With the same radius and with Y as a centre, draw another circle using compasses. Let it cuts the previous circle at A and B.
Step 4. Join AB. Then AB¯¯¯¯¯¯¯¯ is the perpendicular bisector of the line segment XY¯¯¯¯¯¯¯¯.
(a) On examination, we find that PX = PY.
(b) We can say that the lengths of MX is half of the length of XY.
Question 4.
Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
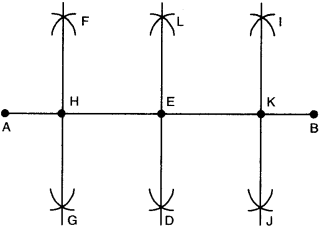

Solution :
Step 1. Draw a line segment AB¯¯¯¯¯¯¯¯ of length 12.8 cm.
Step 2. With A as centre, using compasses, draw two arcs on either side of AB. The radius of this arc should be more than fialf of the length of AB¯¯¯¯¯¯¯¯.
Step 3. With the same radius and with B as centre, draw another arcs using compasses. Let it cut the previous arcs at C and D.
Step 4. Join CD¯¯¯¯¯¯¯¯. It cuts AB¯¯¯¯¯¯¯¯ at E. Then CD¯¯¯¯¯¯¯¯ is the perpendicular bisector of the line segment AB¯¯¯¯¯¯¯¯.
Step 5. With A as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of AE.
Step 6. With the same radius and with E as centre, draw another circle using compasses; Let it cut the previous circle at F and G.
Step 7. Join FG¯¯¯¯¯¯¯¯. It cuts AE¯¯¯¯¯¯¯¯ at H. Then FG¯¯¯¯¯¯¯¯ is the perpendicular bisector of the line segment AE¯¯¯¯¯¯¯¯.
Step 8. With E as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of EB.
Step 9. With the same radius and with B as centre, draw another circle using compasses. Let it cut the previous circle at I and J.
Step 10. Join IJ¯¯¯¯¯¯. It cuts EB¯¯¯¯¯¯¯¯ at K. Then IJ¯¯¯¯¯¯ is the perpendicular bisector of the line segment EB¯¯¯¯¯¯¯¯. Now, the points H, E and K divide AB into four equal parts, i.e., AH¯¯¯¯¯¯¯¯ = HE¯¯¯¯¯¯¯¯ = EK¯¯¯¯¯¯¯¯ = KB¯¯¯¯¯¯¯¯ By measurement, AH¯¯¯¯¯¯¯¯ = HE¯¯¯¯¯¯¯¯ = EK¯¯¯¯¯¯¯¯ = KB¯¯¯¯¯¯¯¯ = 3.2 cm.
Question 5.
With PQ¯¯¯¯¯¯¯¯ of length 6.1 cm as diameter draw a circle.
Solution :
Step 1. Draw a line segment PQ¯¯¯¯¯¯¯¯ of length 6.1 cm.
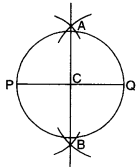

Step 2. With P as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of PQ¯¯¯¯¯¯¯¯.
Step 3. With the same radius and with Q as centre, draw another circle using compasses. Let it cut the previous circle at A and B.
Step 4. Join AB¯¯¯¯¯¯¯¯. It cuts PQ¯¯¯¯¯¯¯¯ at C. Then AB¯¯¯¯¯¯¯¯ is
the perpendicular bisector of the line segment PQ .
Step 5. Place the pointer of the compasses at C and open the pencil upto P.
Step 6. Turn the compasses slowly to draw the circle.
Question 6.
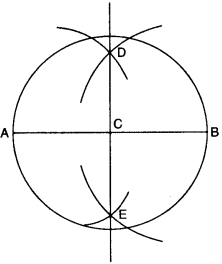
Draw a circle with centre C and radius, 3.4 cm. Draw any chord AB¯¯¯¯¯¯¯¯. Construct the perpendicular bisector of AB¯¯¯¯¯¯¯¯ and examine if it passes through C.
Solution :

Step 1. Draw a point with a sharp pencil and mark it as C.
Step 2. Open the compasses for the required radius 3.4 cm, by putting the pointer on 0 and opening the pencil upto 3.4 cm.
Step 3. Place the pointer of the compasses at C. Step 4. Turn the compasses slowly to draw the
circle.
Step 5. Draw any chord AB¯¯¯¯¯¯¯¯ of this circle.
Step 6. With A as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of AB¯¯¯¯¯¯¯¯.
Step 7. With the same radius and with B as centre, draw another circle using compasses. Let it cut the previous circle at D and E.
Step 8. Join DE¯¯¯¯¯¯¯¯ . Then DE¯¯¯¯¯¯¯¯ is the perpendicular bisector of the line segment AB¯¯¯¯¯¯¯¯. On examination, we find that it passes through C.
Question 7.
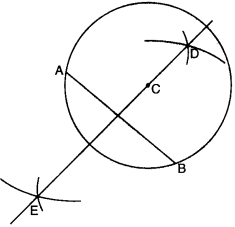
Repeat Question 6, if AB¯¯¯¯¯¯¯¯ happens to be a diameter.
Solution :
Step 1. Draw a point with a sharp pencil and mark it as C.
Step 2. Open the compasses for the required radius 3.4 cm, by putting the pdinter of compasses on 0 of the scale and opening the pencil upto 3.4 cm.
Step 3. Place the pointer of the compasses at C.
Step 4. Turn the compasses slowly to draw the circle.
Step 5. Draw any diameter AB¯¯¯¯¯¯¯¯.

Step 6. With A as centre, using compasses, draw arcs on either side. The radius of this arc should be more than half of the length of AB¯¯¯¯¯¯¯¯.
Step 7. With the same radius and with B as centre, draw another arcs using compasses. Let it cut the previous arcs at D and E.
Step 8. Join DE¯¯¯¯¯¯¯¯ . Then DE¯¯¯¯¯¯¯¯ is the perpendicular bisector of the line segment AB¯¯¯¯¯¯¯¯. On examination, we find that it passes through C.
Question 8.
Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet?
Solution :
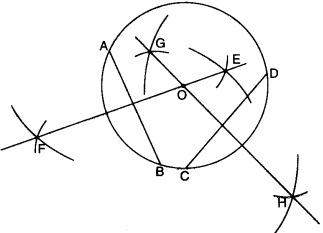

Step 1. Draw a point with a sharp pencil and mark it as O.
Step 2. Open the compasses for the required radius of 4 cm. by putting the pointer on 0 and opening the pencil upto 4 cm.
Step 3. Place the pointer of the compasses at O.
Step 4. Turn the compasses slowly to draw the circle.
Step 5. Draw any two chords AB¯¯¯¯¯¯¯¯ and CD¯¯¯¯¯¯¯¯ of this circle.
Step 6. With A as centre, using compasses, draw two arcs on either side of AB. The radius of this arc should be more than half of the length of AB¯¯¯¯¯¯¯¯.
Step 7. With the same radius and with B as centre, draw another two arcs using compasses. Let it cut the previous circle at E and F.
Step 8. Join EF¯¯¯¯¯¯¯¯. Then EF¯¯¯¯¯¯¯¯ is the perpendicular bisector of the chord AB¯¯¯¯¯¯¯¯.
Step 9. With C a< centre, using compasses, draw two arcs on either side of CD. The radius of this arc should be more than half of the length of CD¯¯¯¯¯¯¯¯.
Step 10. With the same radius and with D as centre, draw another two arcs using compasses. Let it cut the previous circle at G and H.
Step 11. Join GH¯¯¯¯¯¯¯¯. Then GH¯¯¯¯¯¯¯¯ is the perpendi¬cular bisector of the chord CD¯¯¯¯¯¯¯¯. We find that the perpendicular bisectors EF¯¯¯¯¯¯¯¯ and GH¯¯¯¯¯¯¯¯ meet at O, the centre of the circle.
Question 9.
Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA- OB. Draw the perpendicular bisectors of OA¯¯¯¯¯¯¯¯ and OB¯¯¯¯¯¯¯¯. Let them meet at P. Is PA = PB?
Solution :
Step 1. Draw any angle POQ with vertex O.
Step 2. Take a point A on the arm OQ and another point B on the arm OP such that OA¯¯¯¯¯¯¯¯ = OB¯¯¯¯¯¯¯¯.
Step 3. With O as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of OA¯¯¯¯¯¯¯¯.
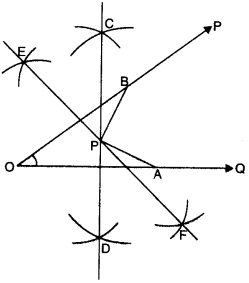

Step 4. With the same radius and with A as centre, draw another circle using compasses. Let it cut the previous circle at C and D.
Step 5. Join CD¯¯¯¯¯¯¯¯. Then CD¯¯¯¯¯¯¯¯ is the perpendicular bisector of the line segment OA¯¯¯¯¯¯¯¯.
Step 6. With O as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of OB¯¯¯¯¯¯¯¯.
Step 7. With the same radius and with B as centre, draw another circle using compasses. Let it cut the previous circle at E and F.
Step 8. Join EF¯¯¯¯¯¯¯¯. Then EF¯¯¯¯¯¯¯¯ is the perpendicular bisector of the line segment OB. The two perpendicu¬lar bisectors meet at P.
Step 9. Join PA¯¯¯¯¯¯¯¯ and PB¯¯¯¯¯¯¯¯. We find that PA¯¯¯¯¯¯¯¯ = PB¯¯¯¯¯¯¯¯.
