ncert solutions for class 6 maths chapter 10 mensuration ex 10.3 ncert class 6 maths chapter 10 exercise 10.3 ncert solutions for class 6 maths chapter 10 mensuration exercise 10.3 ncert solutions for class 6 maths chapter 10 exercise 10.3 ncert solutions class 6 maths chapter 10 exercise 10.3 ncert maths class 6 chapter 10 exercise 10.3 mensuration exercise 10.3 ncert class 6 maths exercise 10.3 solution class 6th maths 10.3 class 6th maths ex 10.3
NCERT Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.3
Question 1.
Find the areas of the rectangles whose sides are:
(a) 3 cm and 4 cm
(b) 12 m and 21m
(c) 2 km and 3 km
(d) 2 m and 70 cm.
Solution :
(a) Area of the rectangle
= Length × Breadth = 3 × 4 sq cm = 12 sq cm
(b) Area of the rectangle = Length × Breadth
= 12 m × 21 m = 252 sq m
(c) Area of the rectangle = Length × Breadth
= 2 km × 3 km = 6 sq km
(d) 2 m = 2 × 100 cm = 200 cm
Area of the rectangle = Length × Breadth
= 200 × 70 sq cm
14000 sq cm.
Question 2.
Find the areas of the squares whose sides are:
(a) 10 cm
(b) 14 cm
(c) 5 m.
Solution :
(a) Area of the square = Side × Side
= 10 cm × 10 cm – 100 sq cm
(b) Area of the square = Side × Side
= 14 cm × 14 cm = 196 sq cm
(c) Area of the square = Side × Side
= 5 m × 5 m = 25 sq m.
Question 3.
The length and breadth of three rectangles are as given below:
(a) 9 m and 6 m
(b) 3 m and 17 m
(c) 4 m and 14 m.
Which one has the largest area and which one has the smallest?
Solution :
(a) Area of the rectangle = Length × Breadth = 9 m × 6 m = 54 sq m
(b) Length of the rectangle = Length × Breadth = 3 m × 17 m = 51 sq m
(c) Length of the rectangle = Length × Breadth = 4m × 14m = 56 sq m
The rectangle (c) has the largest area and the rectangle (b) has the smallest area.
Question 4.
The area of a rectangular garden 50 m long is 300 sq. m. Find the width of the garden.
Solution :
Area of the rectangular garden = 300 sq m Length of the rectangular garden = 50 m
∴ Width of the rectangular garden


Question 5.
What is the cost of tiling a rectangular piece of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred sq m.
Solution :
Length of the rectangular piece of land
500 m
Breadth of the rectangular piece of land
200 m
∴ Area of the rectangular piece of land
= Length × Breadth
= 500 m × 200 m
= 100000 sq m
Cost of tiling 100 sq m = ₹ 8100
Cost of tiling 100000 sq m
= ₹ 8100 × 100000
= ₹ 8000.
Question 6.
A table-top measures 2 m by 1 m 50 cm. What is its area in square meters?
Solution :
Length of the table-top = 2 m Breadth of the table-top = 1 m 50 cm = 1.50 m
∴ Area of the table-top
= Length × Breadth = 2 m × 1.50 m
= 3.0 sq m.
Question 7.
A room is 4 m long and 3 m 50 cm wide. How many square meters of carpet is needed to cover the floor of the room?
Solution :
Length of the room = 4 m Breadth of the room = 3 m 50 cm = 3.50 m
∴ Area of the room = Length × Breadth
= 4 × 3.5 sq. m
= 14.0 sq m
Hence, 14.0 square meters of carpet is needed to cover the floor of the room.
Question 8.
A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Solution :
Length of the floor = 5 m Breadth of the floor = 4 m
∴ Area of the floor = Length × Breadth
= 5m × 4m = 20sqm Area of the square carpet = Side × Side
= 3m × 3m = 9sqm
∴ Area of the floor that is not carpeted = 20 sq m – 9 sq m = 11sq m.
Question 9.
Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of land?
Solution :
Area of square flower bed
= Side × Side = 1 m × 1 m
= 1 sq m
∴ Area of 5 square flower beds
= 5 × 1 sq m = 5 sq m
Length of the piece of land = 5 m
Breadth of the piece of land = 4 m
∴ Area of the piece of land
= Length × Breadth = 5 m × 4 m
= 20 sq m
∴ Area of the remaining part of the land
= 20 sq m – 5 sq m
= 15 sqm.
Question 10.
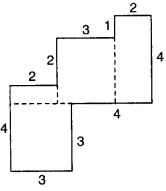
By splitting the following figures into rectangles, find their areas (The measures are given in centimeters).
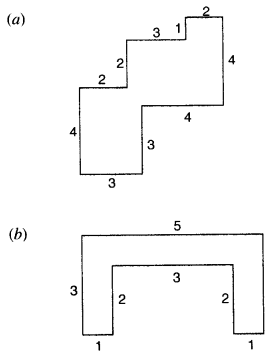

Solution :
(a) Area of the figure
= (3 × 3 + 1 × 2 + 3 × 3 + 4 × 2) sqcm
= (9 + 2 + 9 + 8) sq cm = 28 sq cm

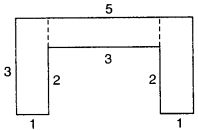
(b) Area of the figure
= (3 × 1 + 3 × 1 + 3 × 1) sqm
= (3 + 3 + 3) sq m
= 9 sqm

Question 11.
Split the following shapes into rectangles and find the area of each (The measures are given in centimeters).
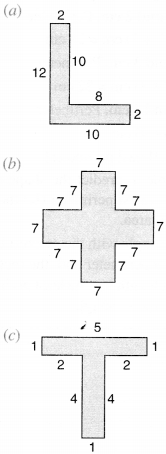

Solution :
(a) Area of the shape
= (8 × 2 + 12 × 2) sq cm = (16 + 24) sq cm = 40 sq cm
(b) Area of the shape
= (17 × 7 + 7 × 7 + 7 × 7 + 7 × 7 + 7 × 7) sq cm
= (49 + 49 + 49 + 49 + 49) sq cm
= 245 sq cm
(c) Area of the shape = ( 5 × 1 + 4 × 1) sq cm
= (5 + 4) sq cm
= 9 sq cm.
Question 12.
How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are respectively :
(a) 100 cm and 144 cm?
(b) 70 cm and 36 cm?
Solution :
(a) Length of the region = 100 cm Breadth of the region = 144 cm
∴ Area of the region = Length × Breadth
= 100 cm × 144 cm
= 14400 sq cm
Length of a tile = 12 cm Breadth of a tile = 5 cm
∴ Area of a tile = Length × Breadth = 12 × 5 sq cm
= 60 sq cm
∴ Number of tiles needed to fit the region


(a) Length of the region = 70 cm Breadth of the region = 36 cm
∴ Area of the rectangular region = 70 × 36 sq cm
= 2520 sq cm Area of a tile = 60 sq cm
∴ Number of tiles needed to fit the region
![]()
![]()
A challenge!
On a centimeter squared paper, make as many rectangles as you can such that the area of the rectangle is 16 sq cm (consider only whole number lengths).
(a) Which rectangle has the greatest perimeter?
(b) Which rectangle has the least perimeter? If you take a rectangle of area 24 sq. cm., what
will be your answers?
Given any area, is it possible to predict the shape of the rectangle with the greatest perimeter? With the least perimeter? Give example and reason.
Solution :
Three rectangles can be made as follows:
(i) Sides 16 cm and 1 cm. Perimeter
= 2 × (Length + Breadth)
= 2 × (16 + 1) cm = 34 cm
(ii) Sides 8 cm and 2 cm. Perimeter
= 2 × (Length + Breadth)
= 2 × (8 + 2) cm = 20 cm
(iii) Sides 4 cm and 4 cm. Perimeter
= 2 × (Length + Breadth)
= 2 (4 + 4) cm = 16 cm
(a) The rectangle (i) has the greatest perimeter.
(b) The rectangle (iii) has the least perimeter.
For Area 24 sq. cm, four rectangles can be made as follows :
(i) Sides 24 cm and 1 cm. Perimeter
= 2 × (24 + 1)cm = 50 cm [Greatest perimeter]
(ii) Sides 12 cm and 2 cm. Perimeter
= 2 × (12 + 2) cm = 28 cm
(iii) Sides 8 cm and 3 cm. Perimeter
= 2 × (8 + 3) cm = 22 cm
(iv) Sides 6 cm and 4 cm. Perimeter
= 2 × (6 + 4) cm = 20 cm [Least perimeter]
Yes ! it is possible to predict the shape of the rectangle with (i) the greatest perimeter (iv) the least perimeter for any given area.
Reason: The rectangle with the greatest length has the maximum perimeter and the rectangle with the smallest length has the least perimeter, for a given area of the rectangle.
